(x y z)^3 identity 572218-(x+y+z)^3 identity

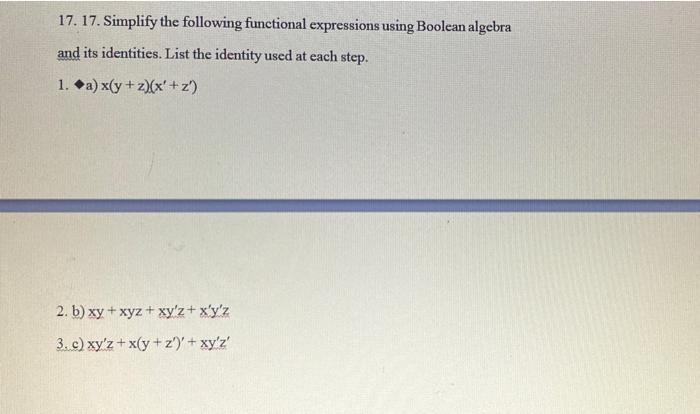
Using the identity and proof x 3y 3z 3−3xyz=(xyz)(x 2y 2z 2−xy−yz−zx)

(x+y+z)^3 identity-Mozaffar Author has 268 answers and 221K answer views Aug 4 Answer The formula for (xyz) ^3 is = x^3y^3z^33 (xy) (yz) (zx) Murali Krishna Former Retired Senior Lecturer inAn elementary approach, without $\text{AM} \ge \text{GM}$ is to use the identity $$x^3 y^3 z^3 3xyz = (xyz)\left(\frac{(xy)^2 (yz)^2 (zx)^2}{2}\right)$$ Thus $$\text{if }

(x+y+z)^3 identityのギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「(x+y+z)^3 identity」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「(x+y+z)^3 identity」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「(x+y+z)^3 identity」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「(x+y+z)^3 identity」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「(x+y+z)^3 identity」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「(x+y+z)^3 identity」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「(x+y+z)^3 identity」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

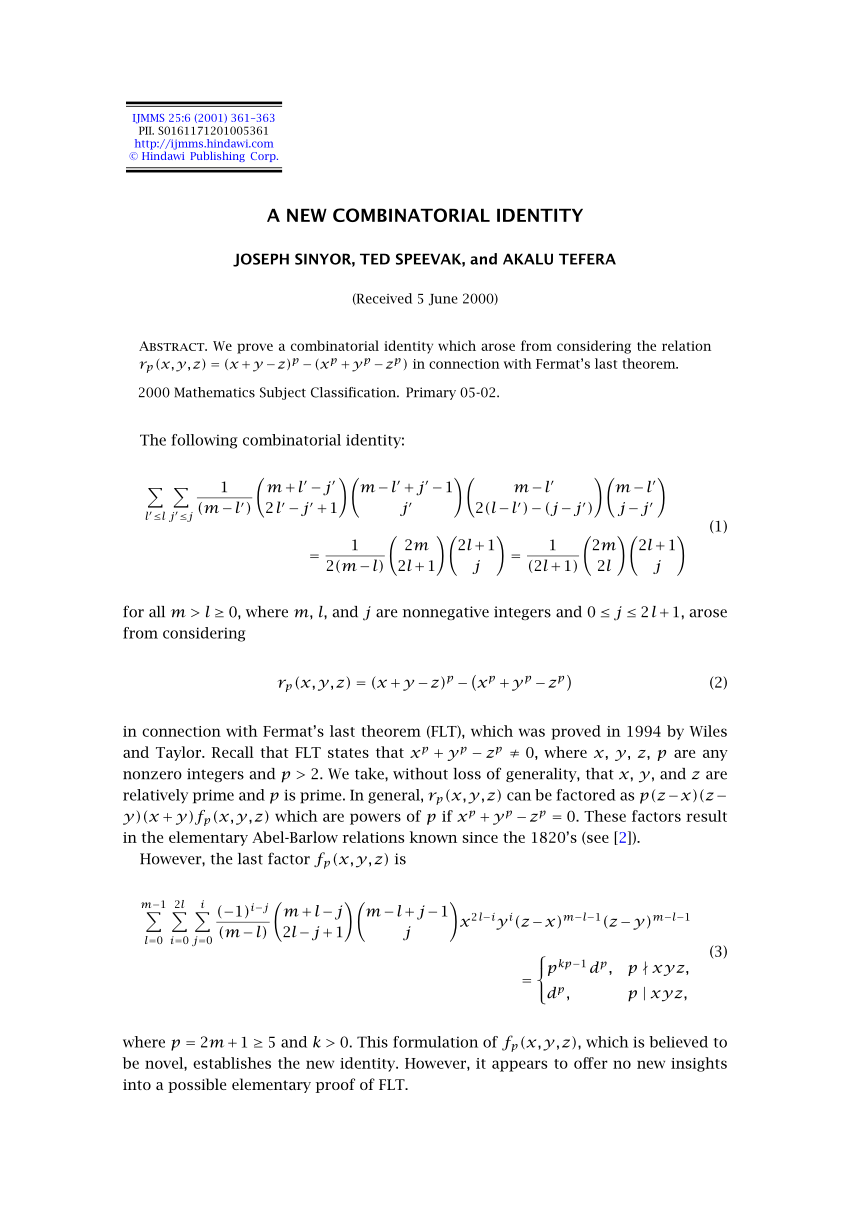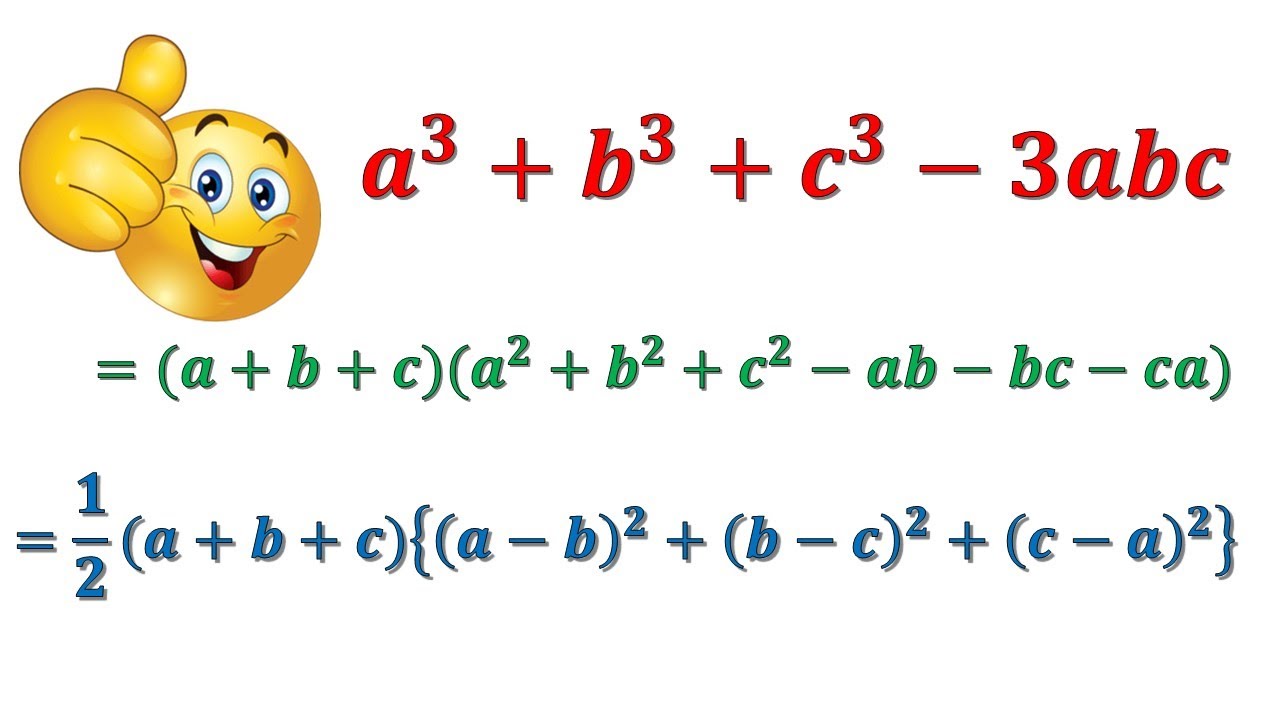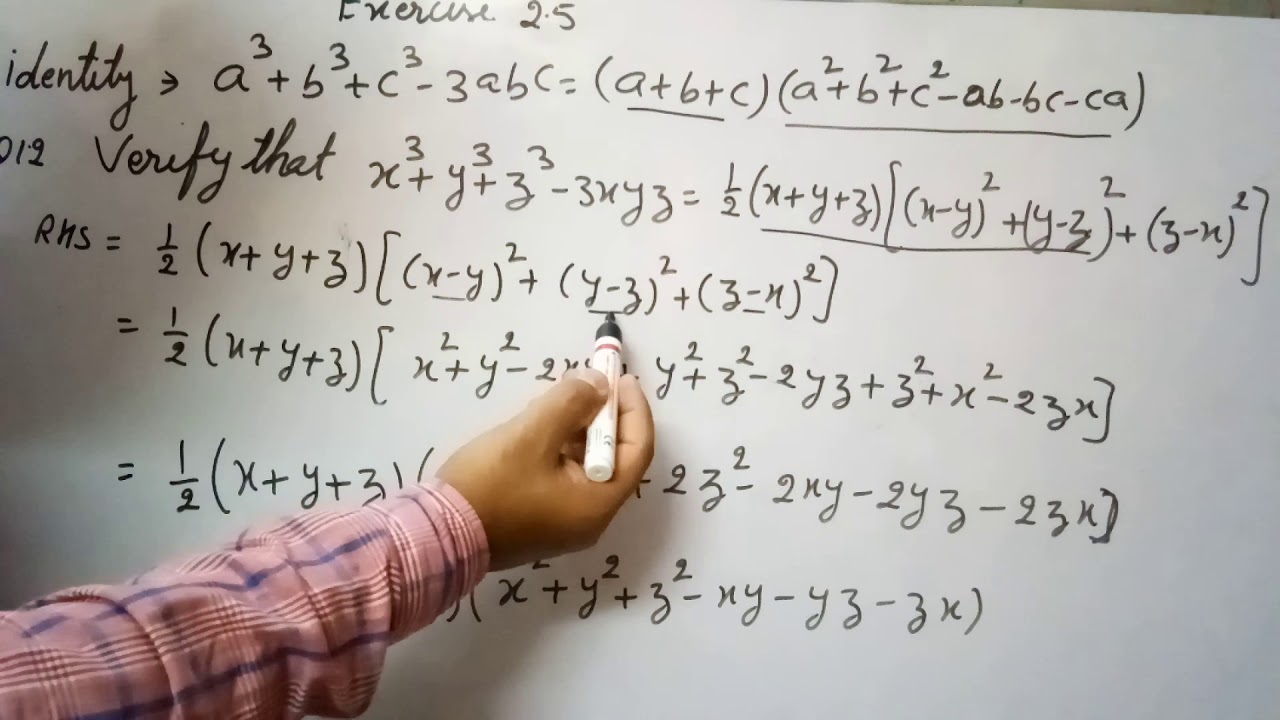「(x+y+z)^3 identity」の画像ギャラリー、詳細は各画像をクリックしてください。

Using the identity and proof x 3 y 3 z 3 − 3 x y z = (x y z) (x 2 y 2 z 2 − x y − y z − z x)Using the identity and proof x 3y 3z 3−3xyz=(xyz)(x 2y 2z 2−xy−yz−zx)

Incoming Term: (x+y+z)^3 identity,